
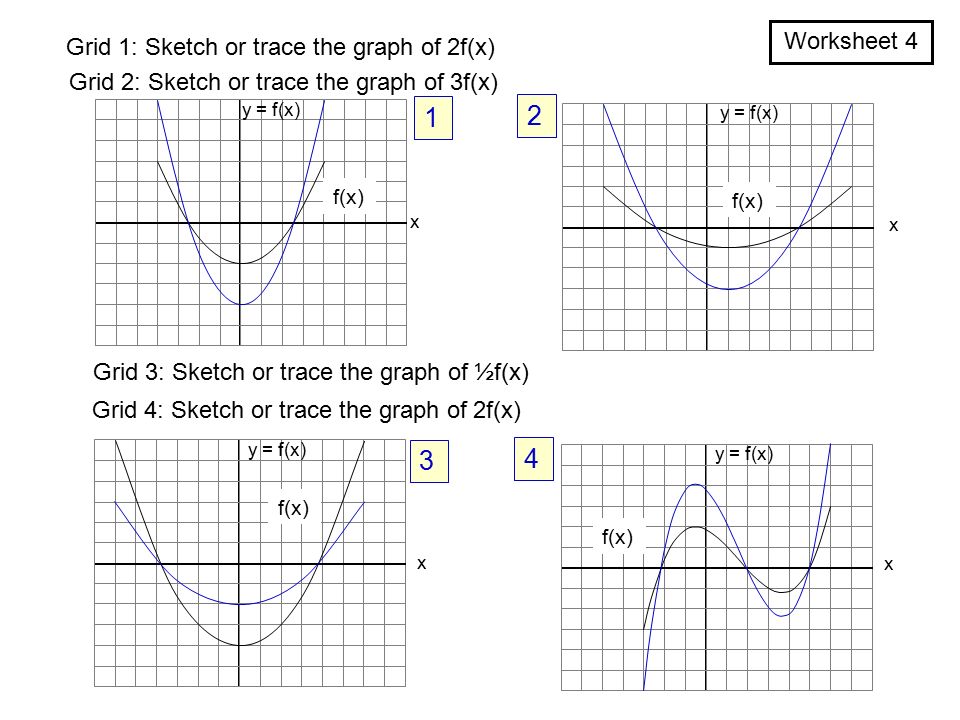
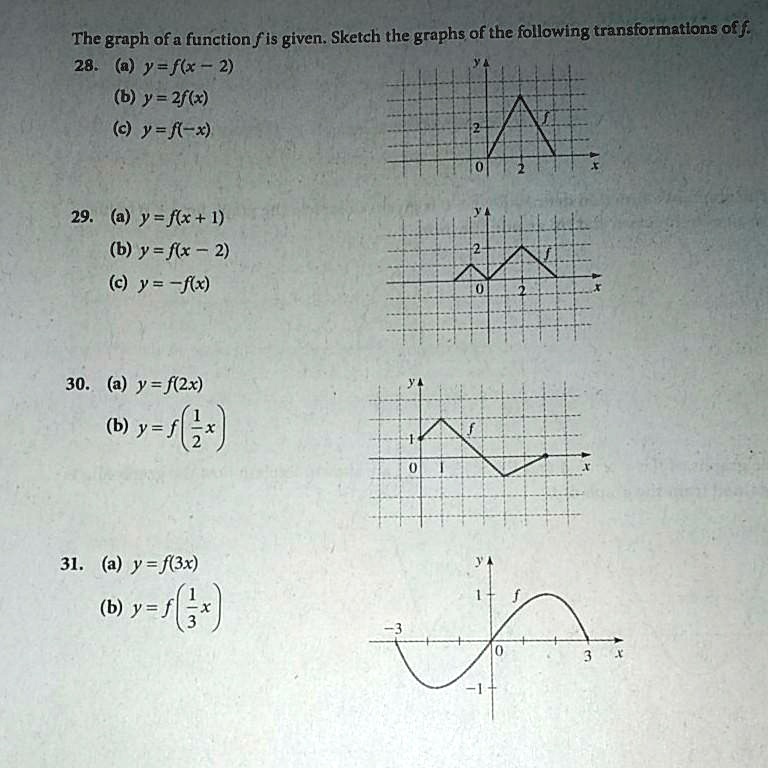
Stretches Of Graphs Iitutor
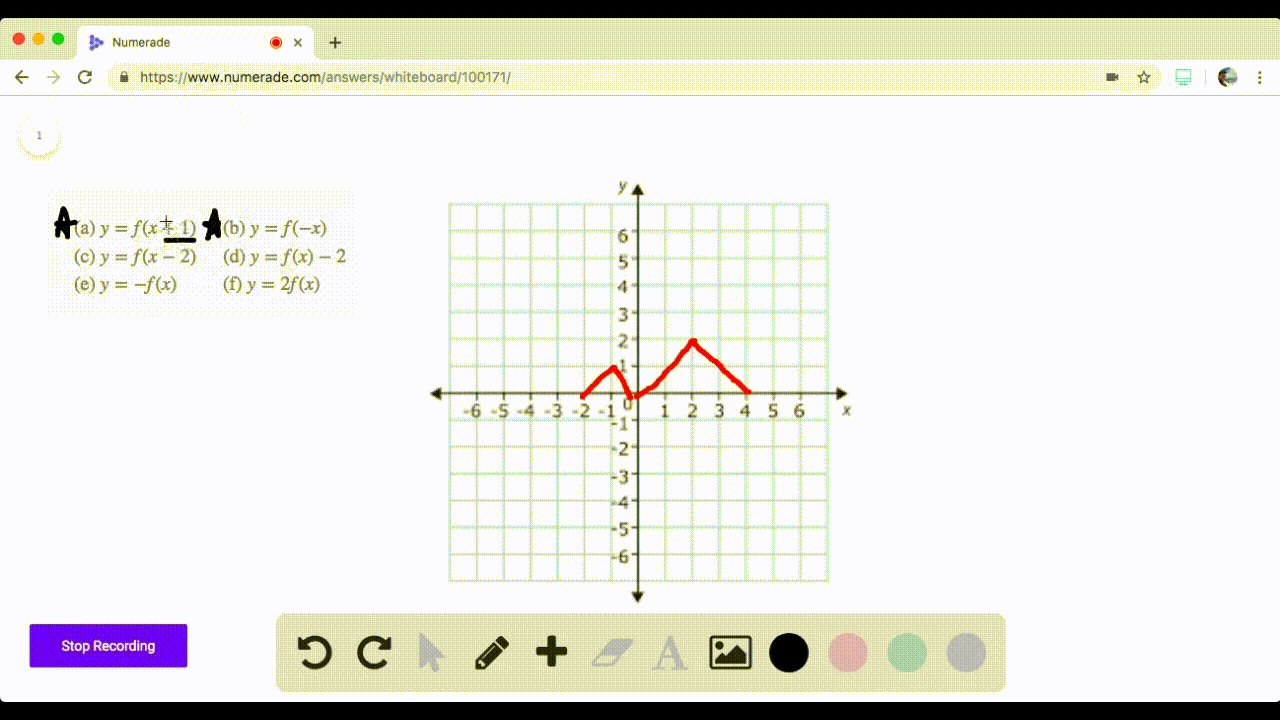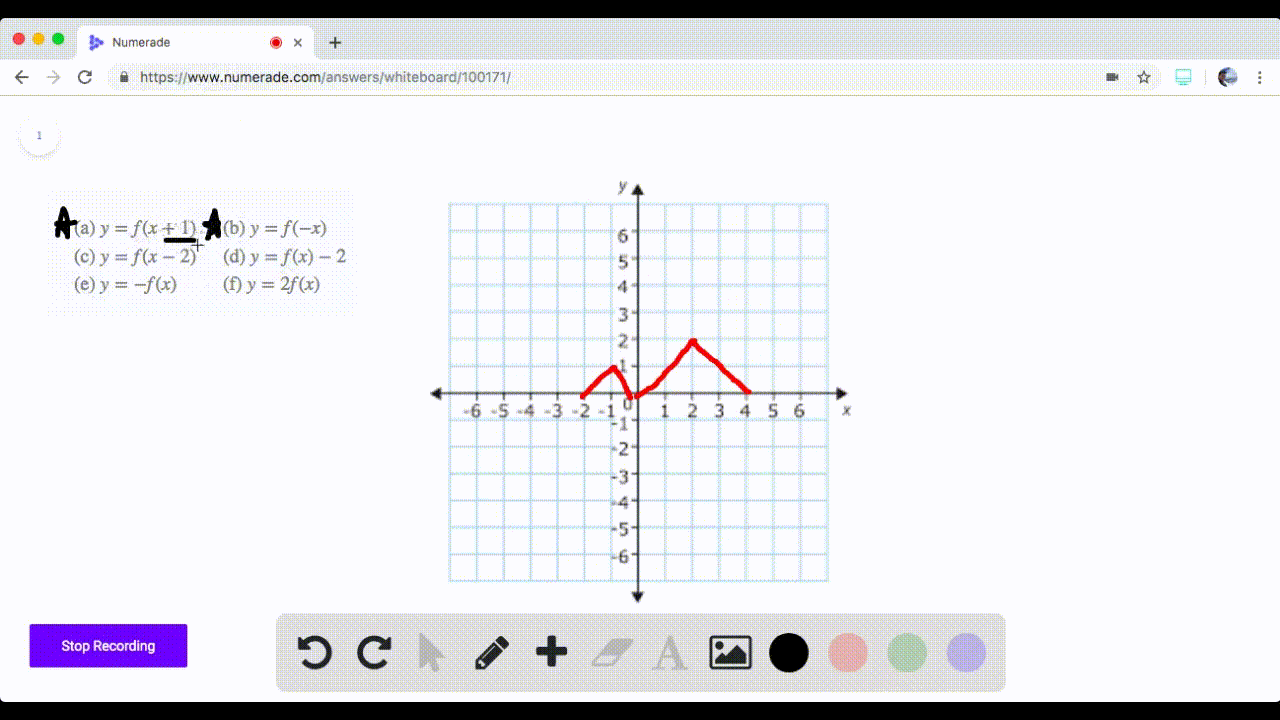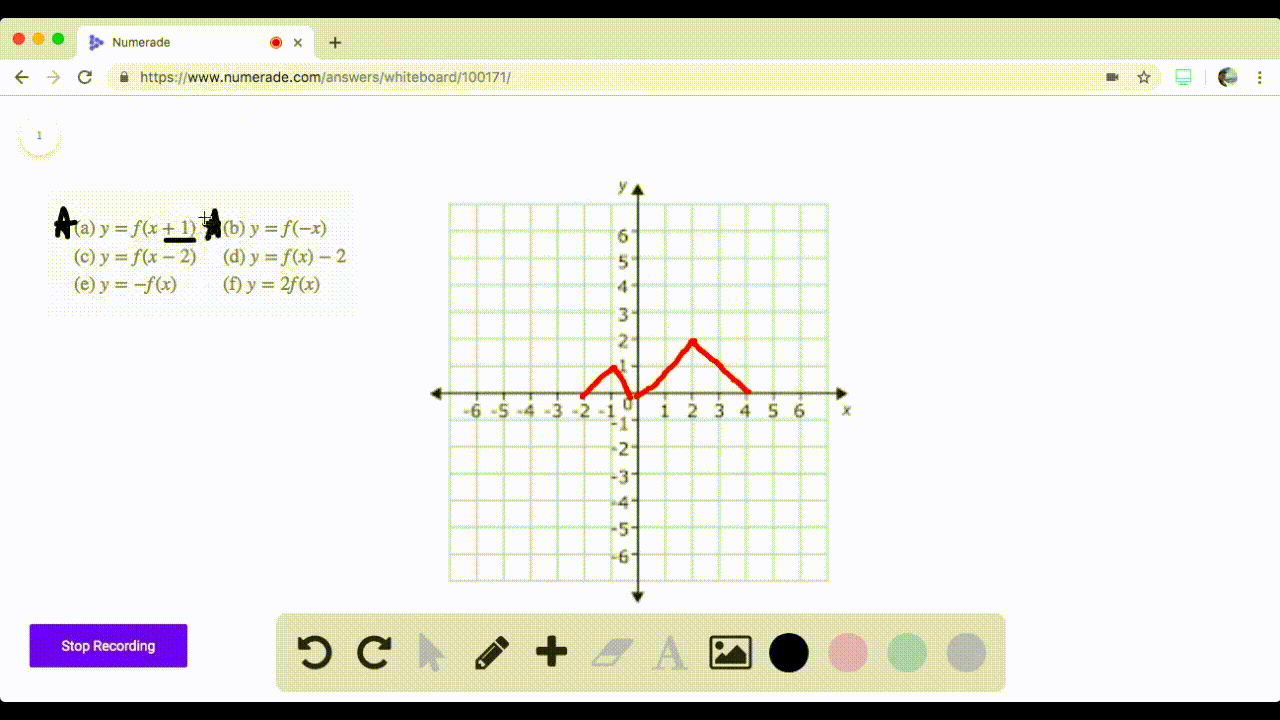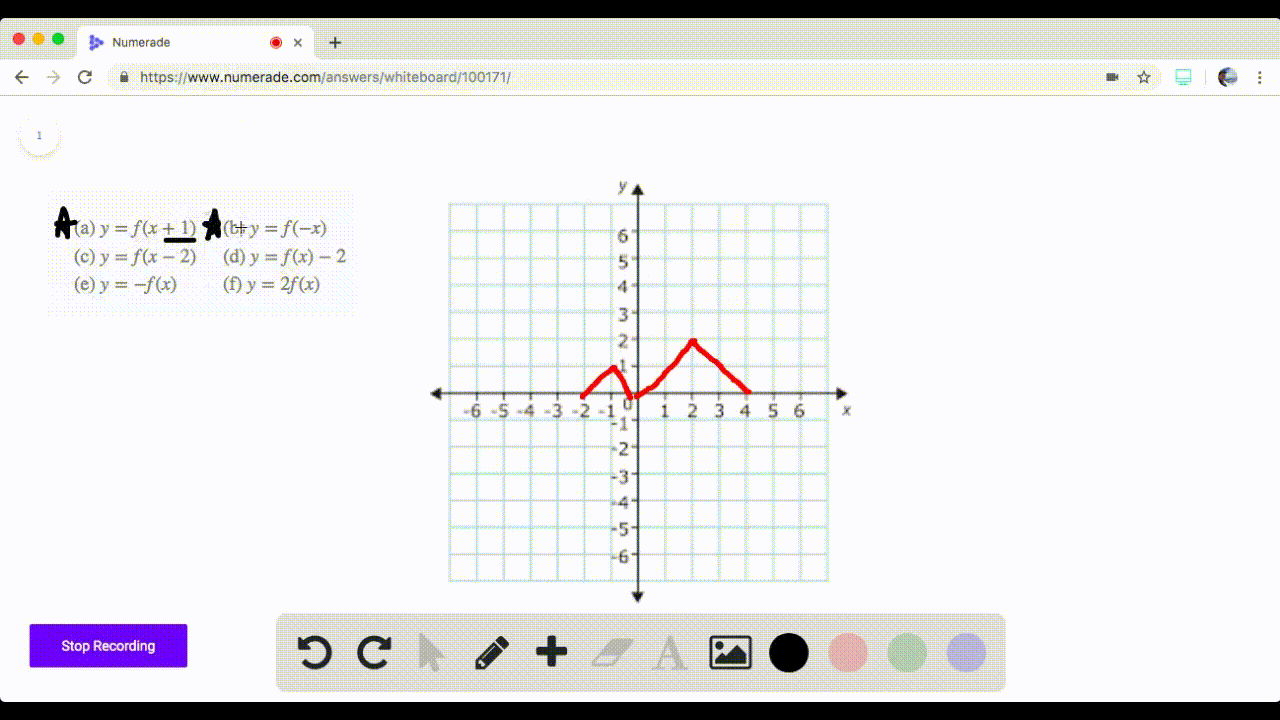
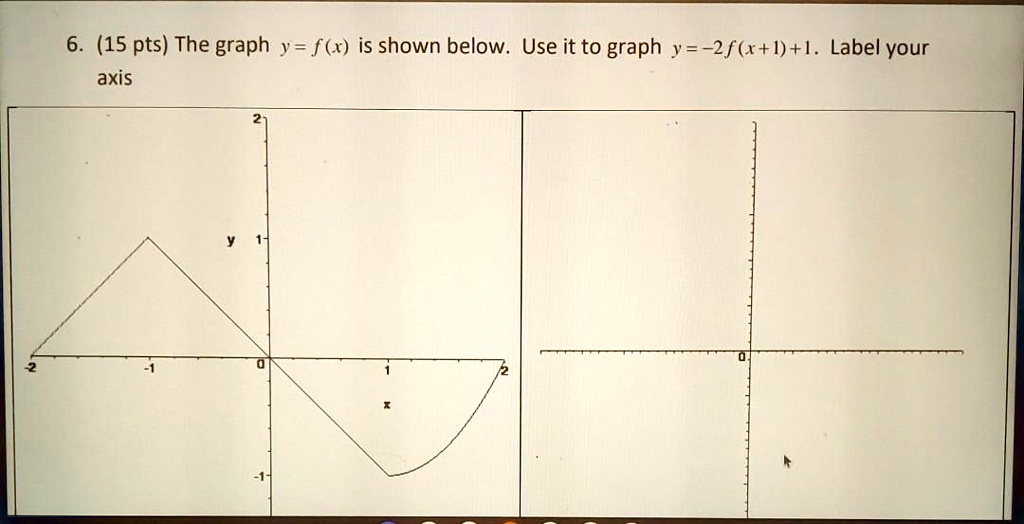
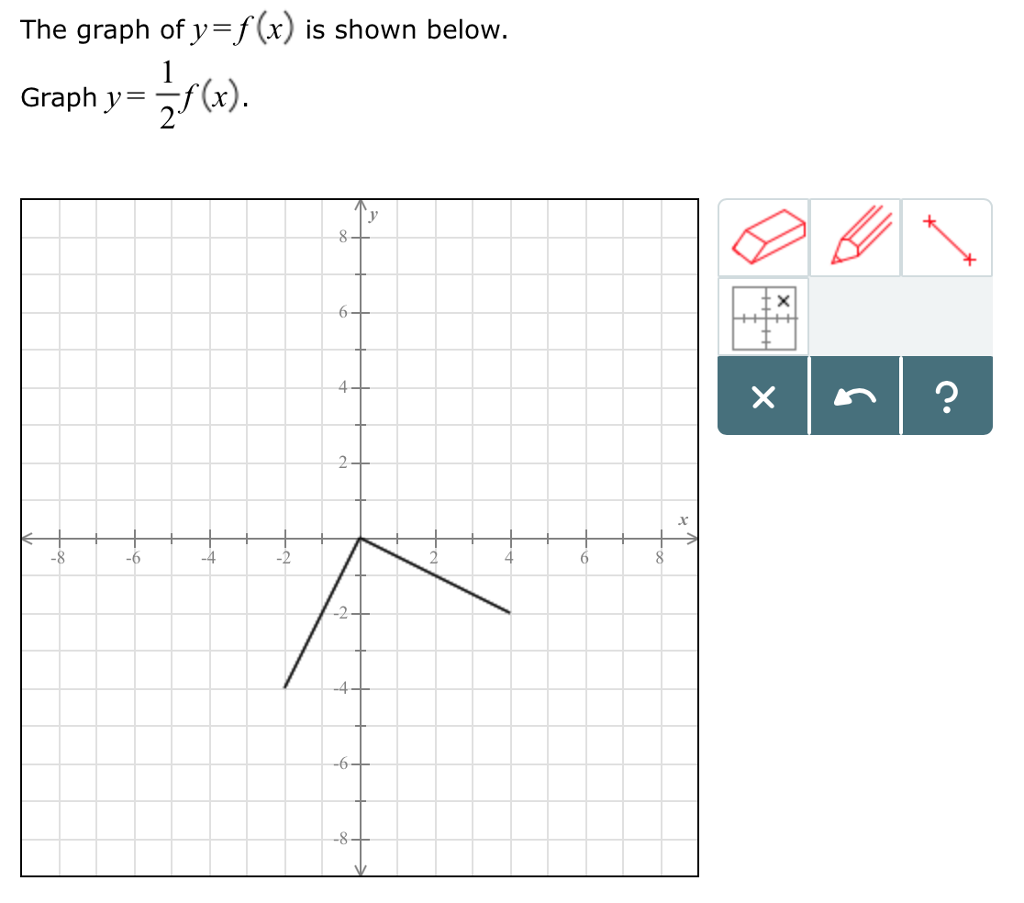
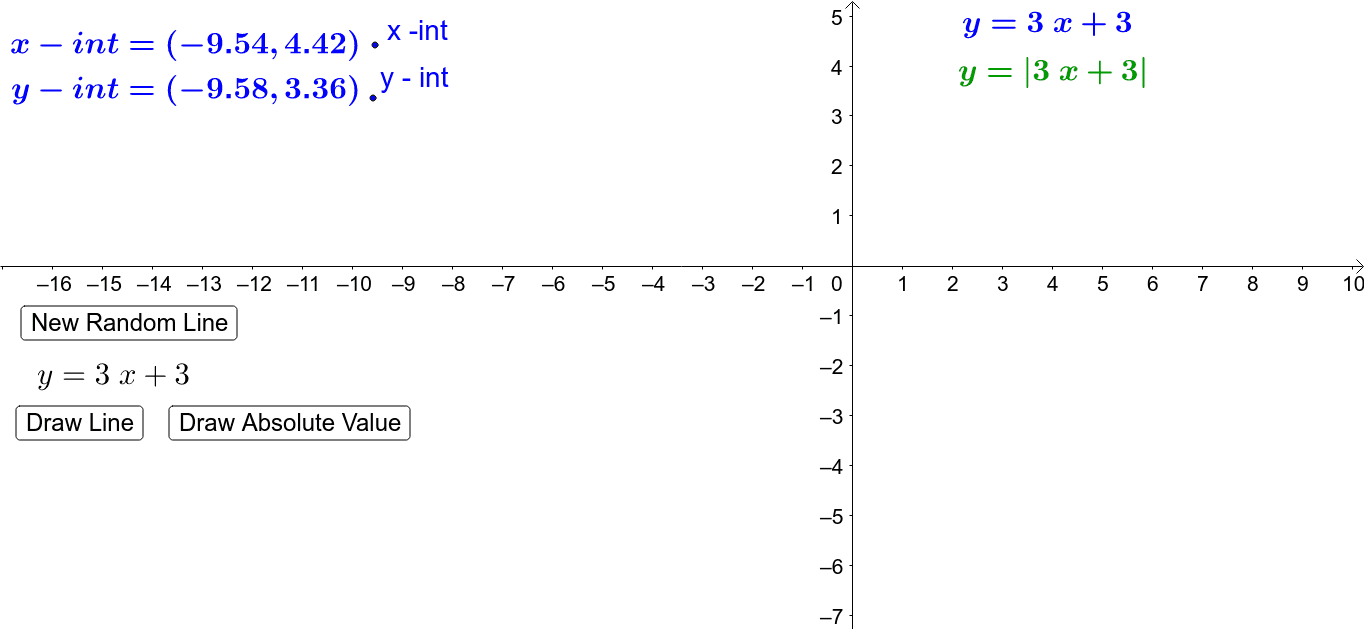
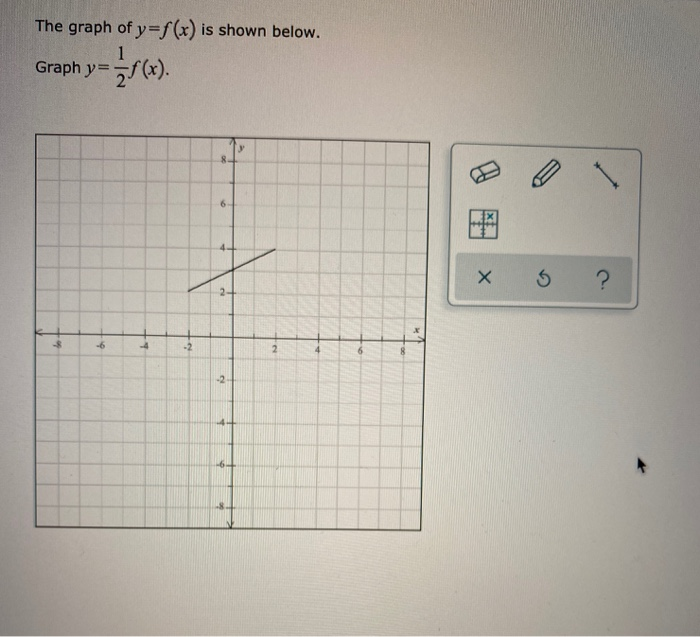
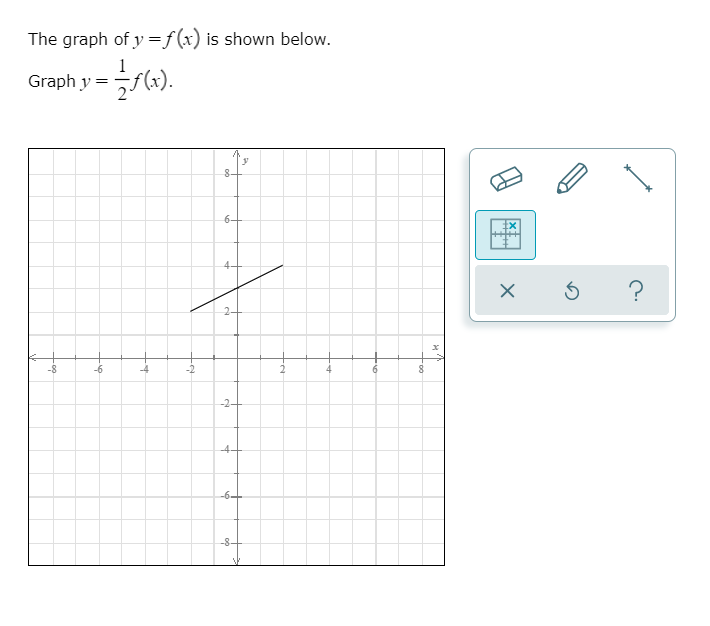
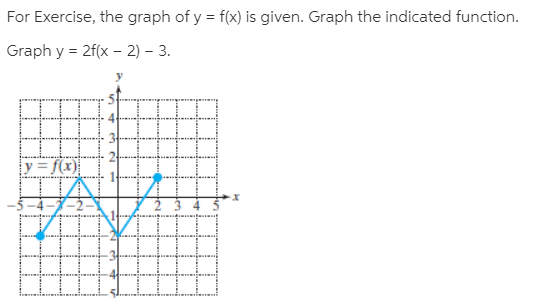
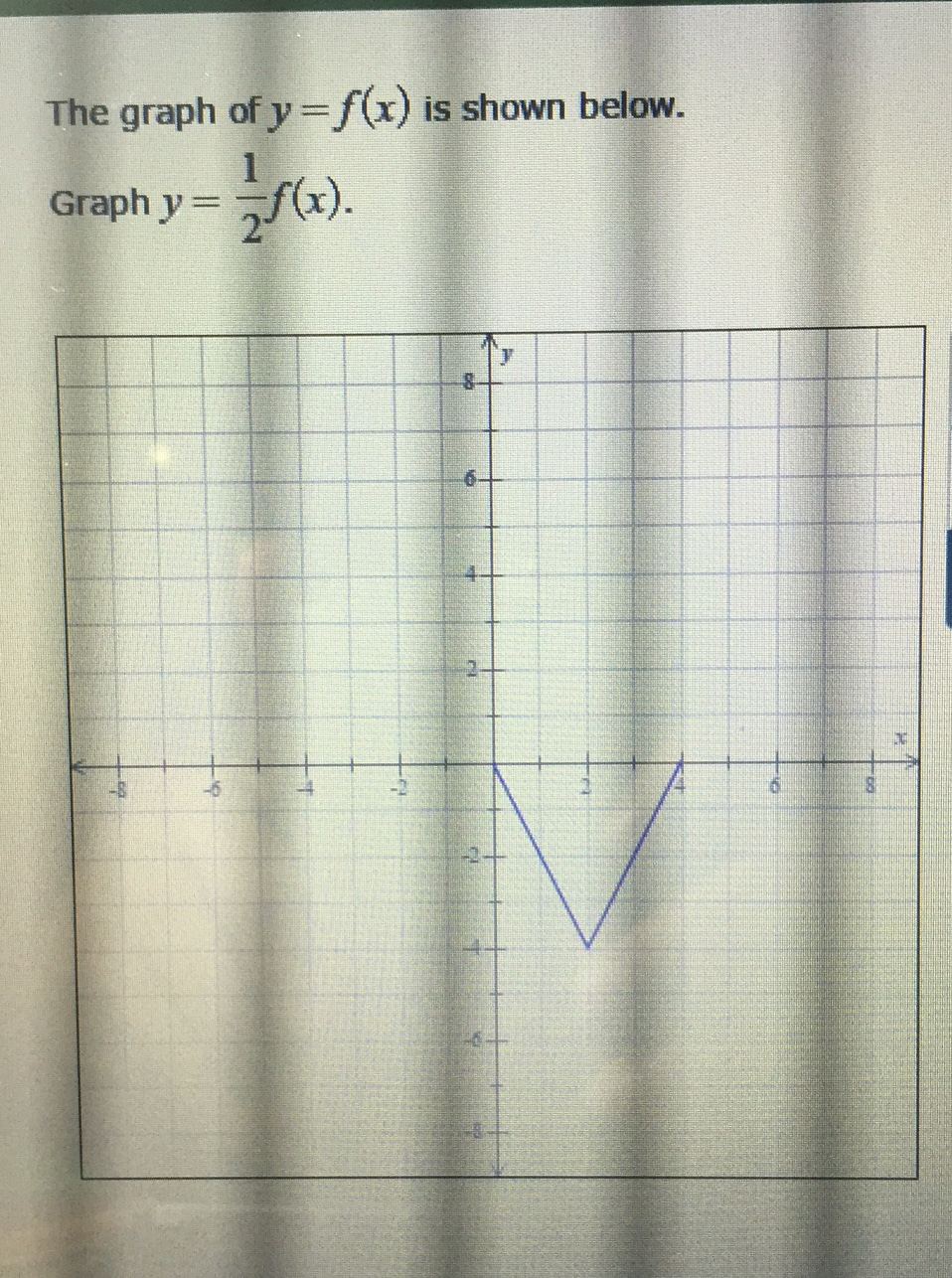
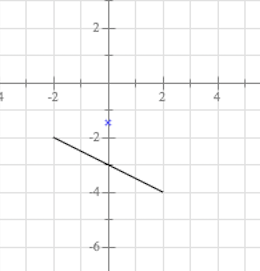
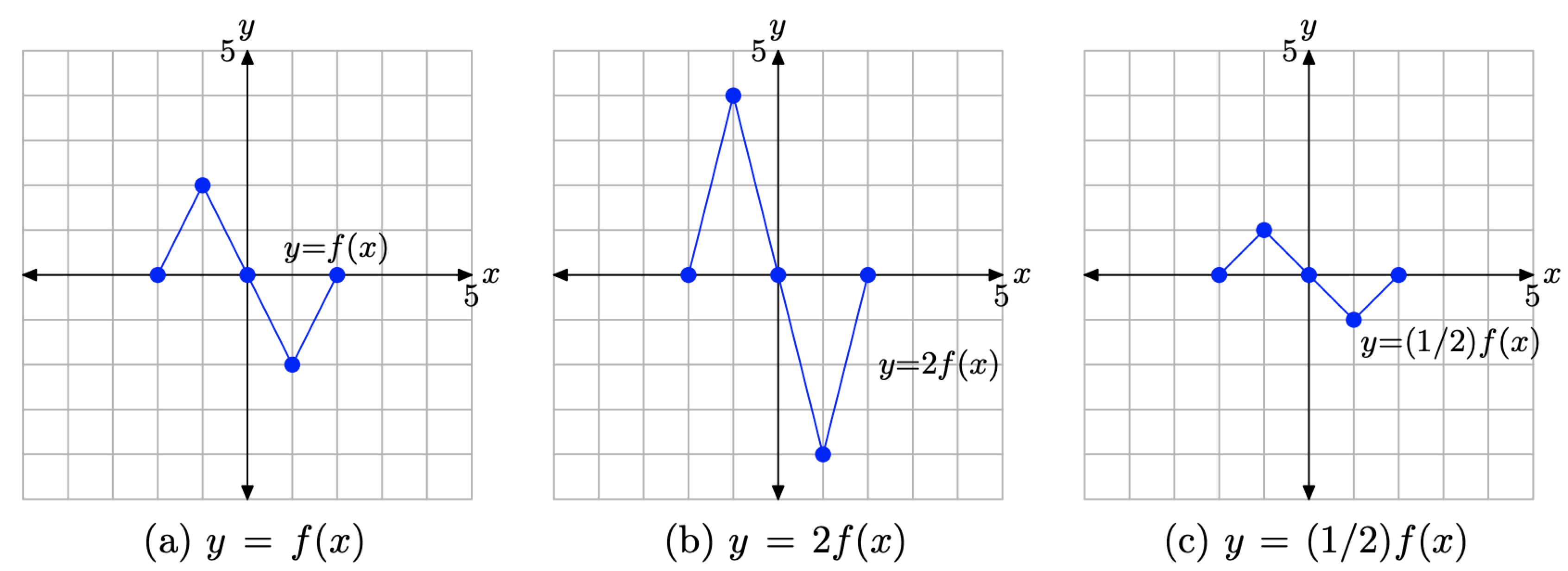
In this video I try to explain what a function in maths is I once asked myself, why keep writing y=f(x) and not just y!??The graph of y = 1/2f(x) is the graph y = x and y = x for 4 ≤ y ≤ 0 Stepbystep explanation Here we note that when y = 0, x = 0 when y = 4, x = 2 The equation is therefore of the form y = m·x c m = slope c = y intercept = 0 Hence the first line is y = 2·x The second line on the right is the mirror of the first on the left
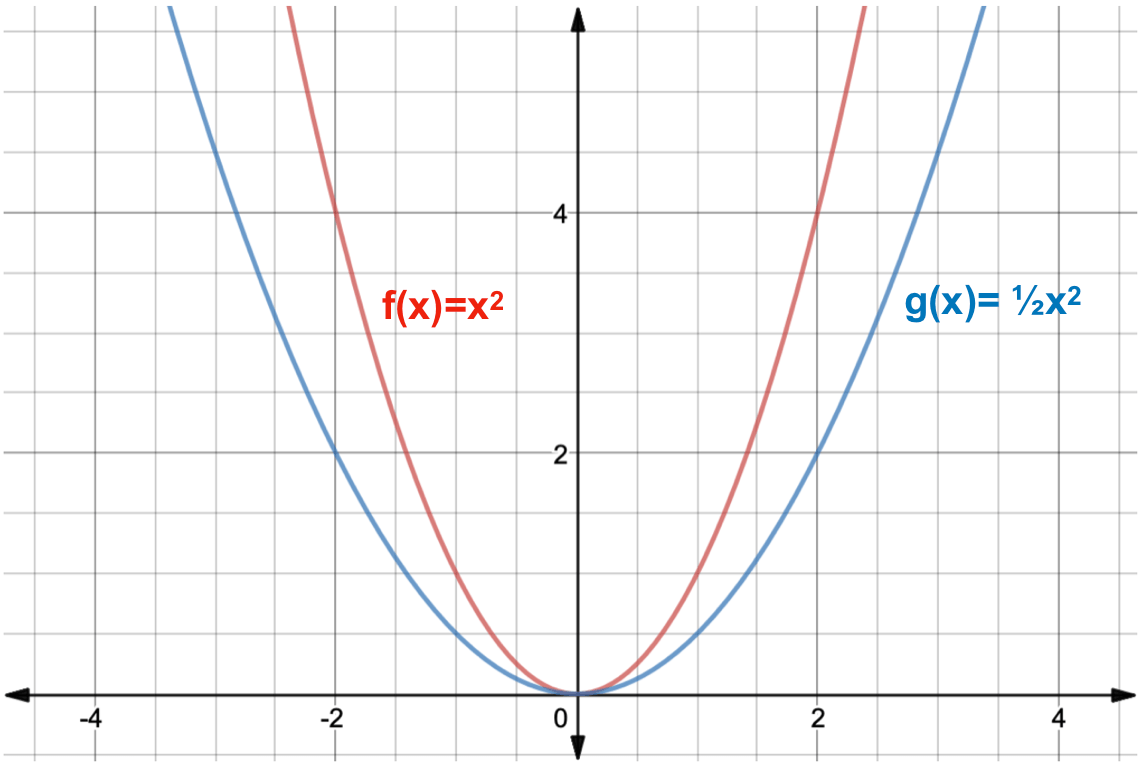
Y=f(x) graph y=1/2f(x)
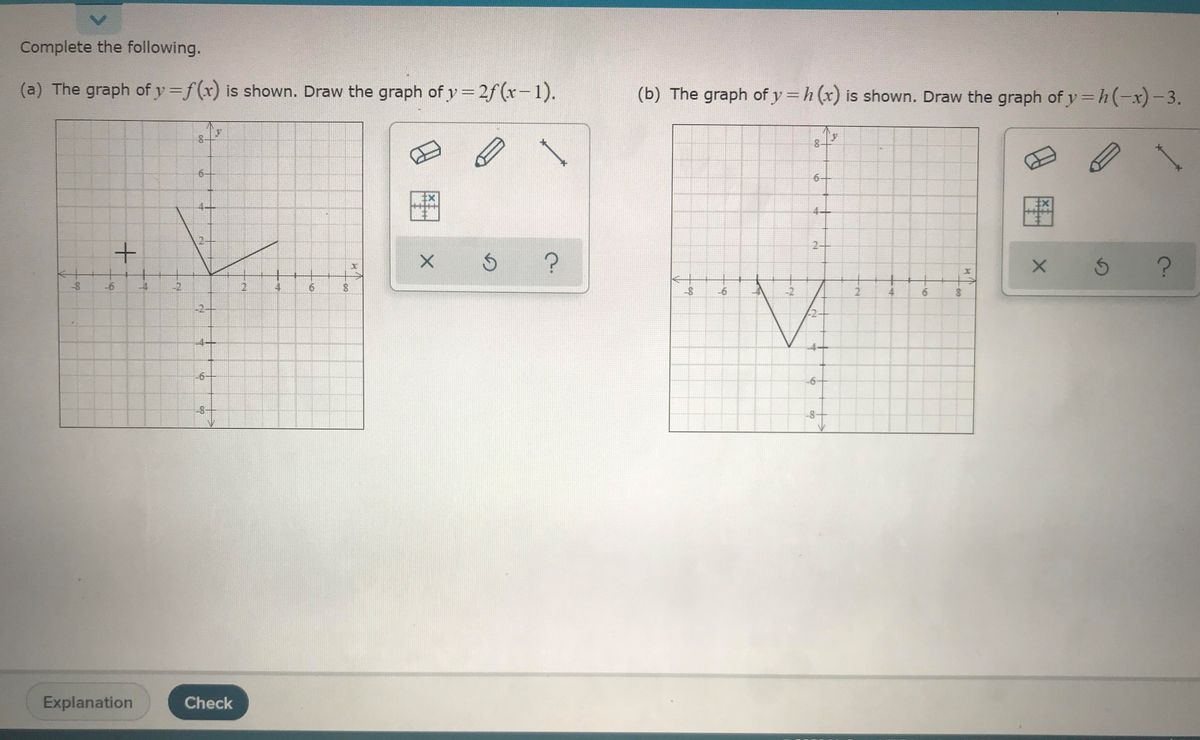
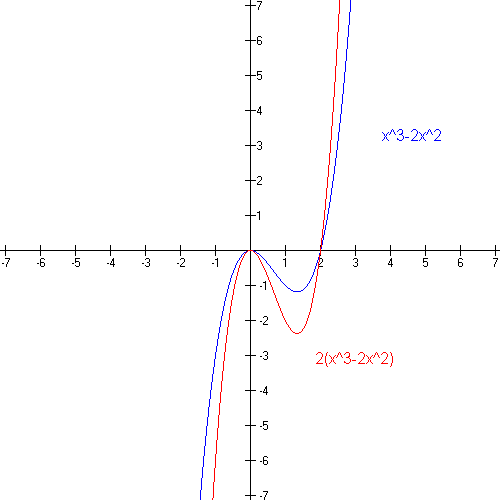
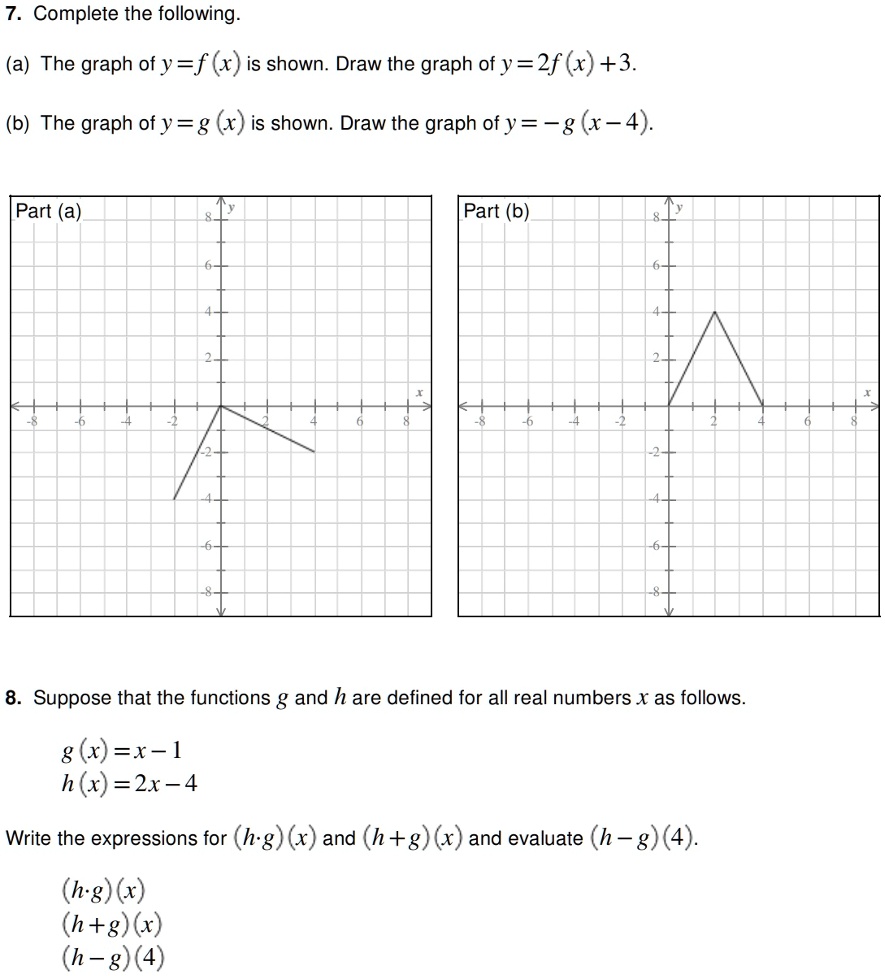
Y=f(x) graph y=1/2f(x)- As you have x2 then 1 x2 will always be positive So y is always positive As x becomes smaller and smaller then 1 1 x2 → 1 1 = 1 So lim x→0 1 1 x2 = 1 As x becomes bigger and bigger then 1 x2 becomes bigger so 1 1 x2 becomes smaller lim x→±∞ 1 1 x2 = 0 build a table of value for different values of x and calculate theThe graph of y = f (x) a has a minimum at (3, 0), where a is a constant (c) Write down the value of a (1) (Total 7 marks) _____ ta C1 Functions – Transformations and Graphs C1 Functions Transformations and Graphs – Questions 3 2 (a) On the axes below sketch the graphs of (i) y
1 2f X Graph Transformation
This video has not been made yet PleaseIf the graph of the function y = f(x) is as shown The graph of y = 1//2(f(x)f(x)) is The graph of the function y= f (x) is symmetrical about the line x=2 then The figure above shows the graph of This problem has been solved!
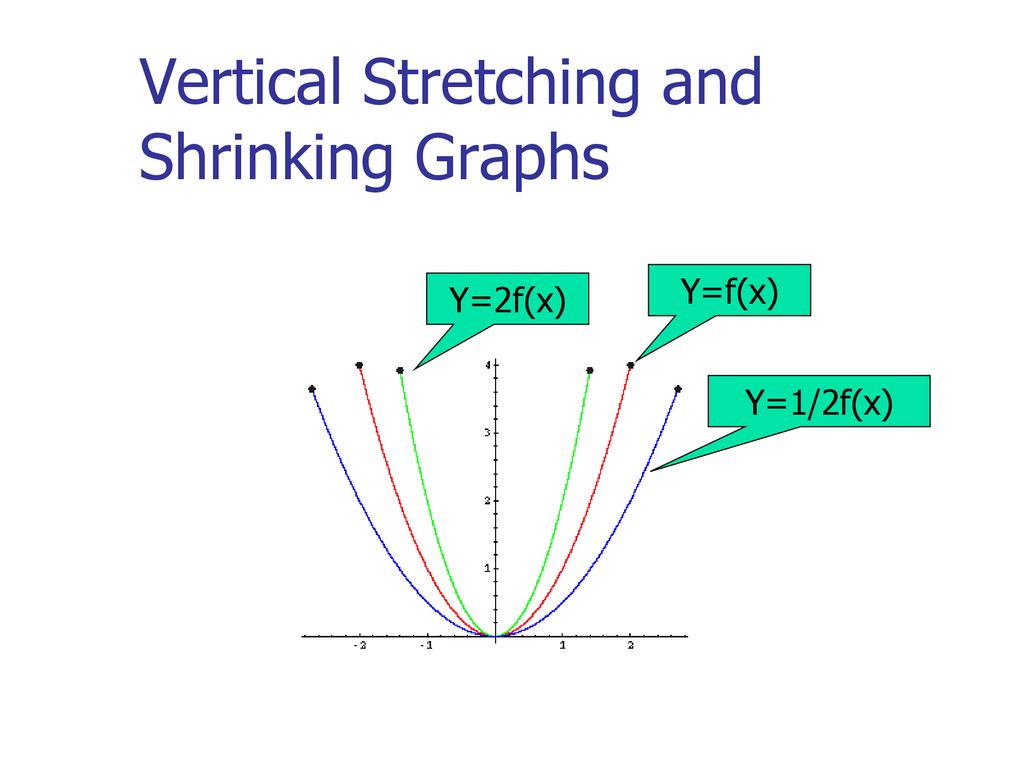
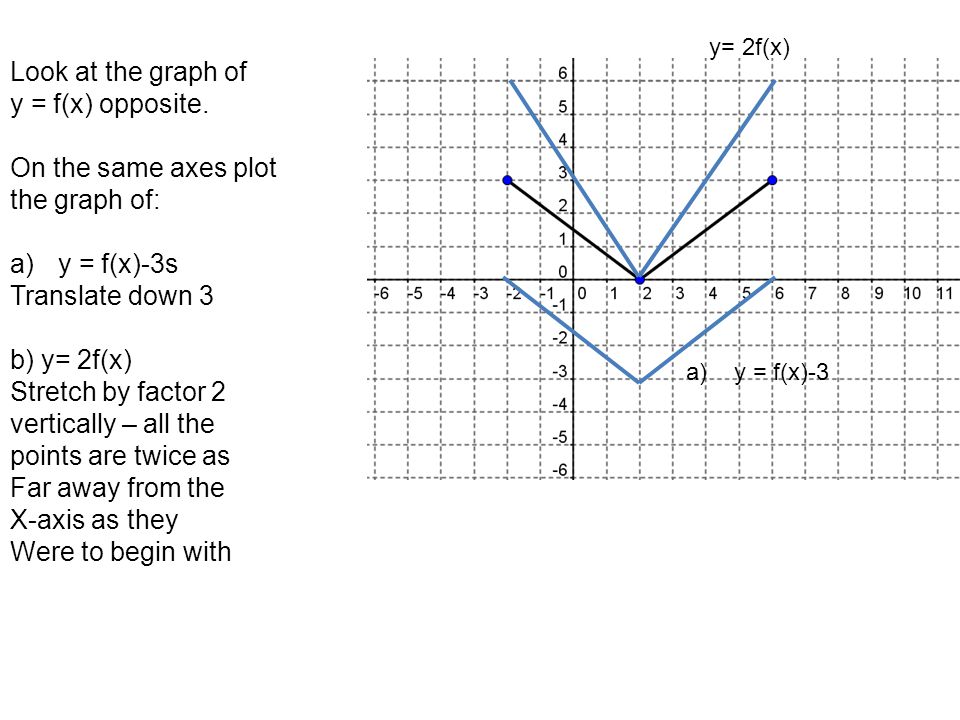
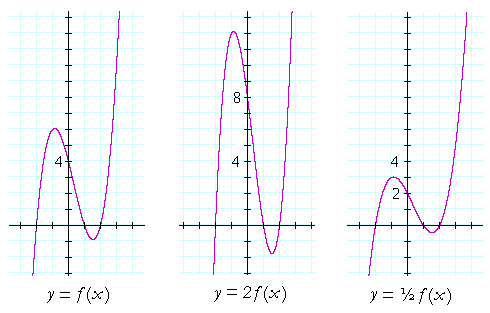
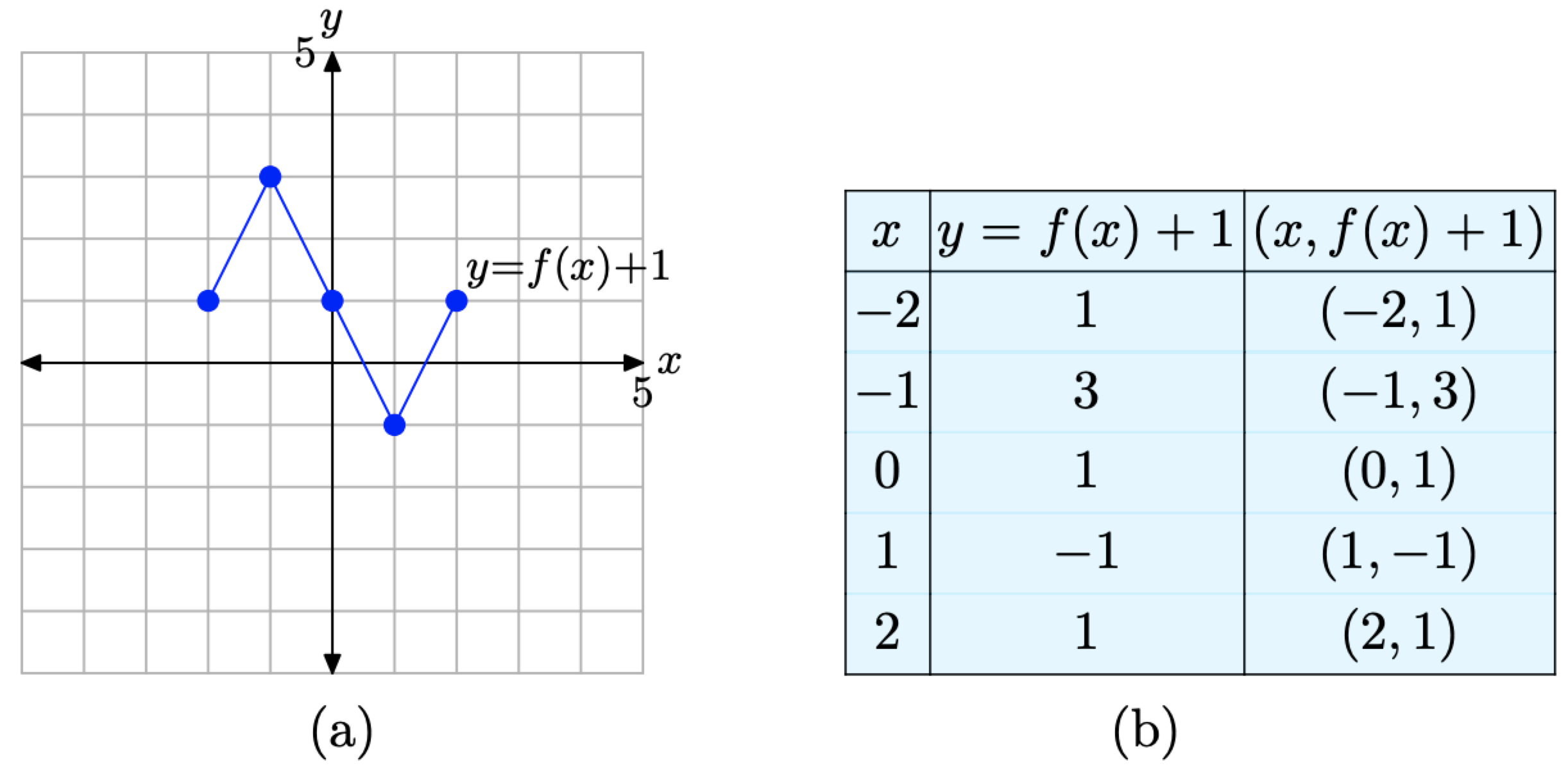
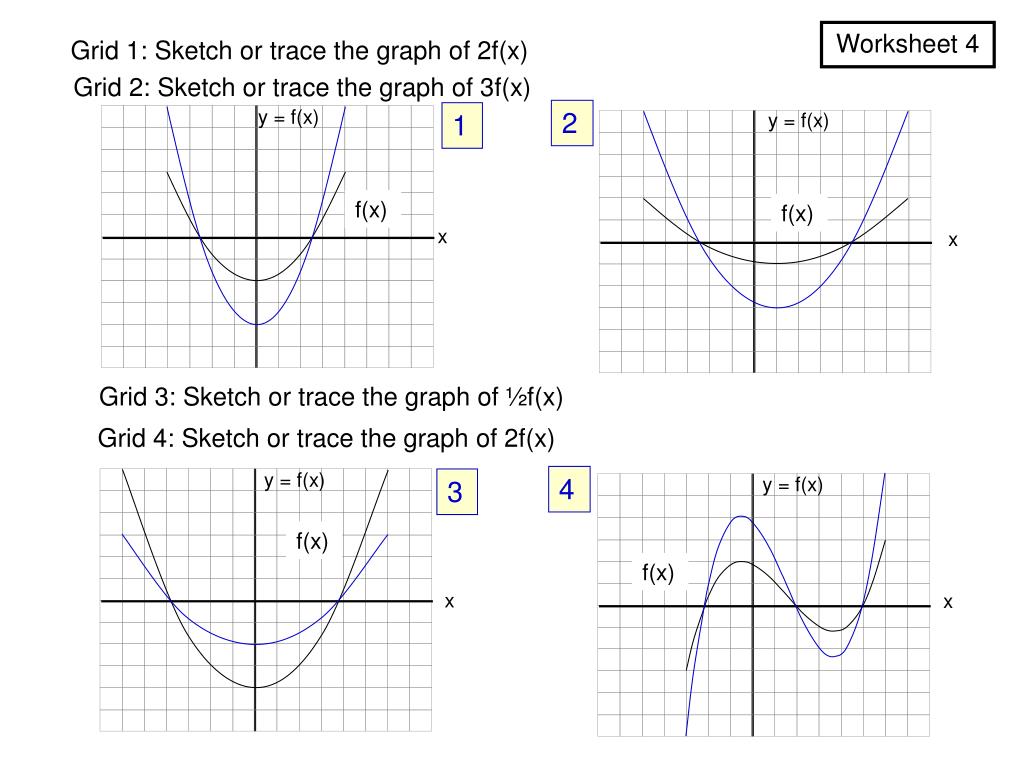
Once I find the value of the first function at x = 3 I multiply this number by 4 to get the value of the second function at x = 2 So look at the points you just identified on the two graphs If you are at the point on the first graph then the corresponding point on the second graph is 5 units to the right and its yvalue is 4 times the yvalue of the point on the first graphFor every value of x, y will be k times larger The graph is y=f (x)Graph y 1 2f x AnswerThe graph of y = 1/2f(x) is the graph y = x and y = x for 4 ≤ y ≤ 0Stepbystep explanation Here we note that when y = 0, x = 0when y = 4,
Y=f(x) graph y=1/2f(x)のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  | |
「Y=f(x) graph y=1/2f(x)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「Y=f(x) graph y=1/2f(x)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「Y=f(x) graph y=1/2f(x)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
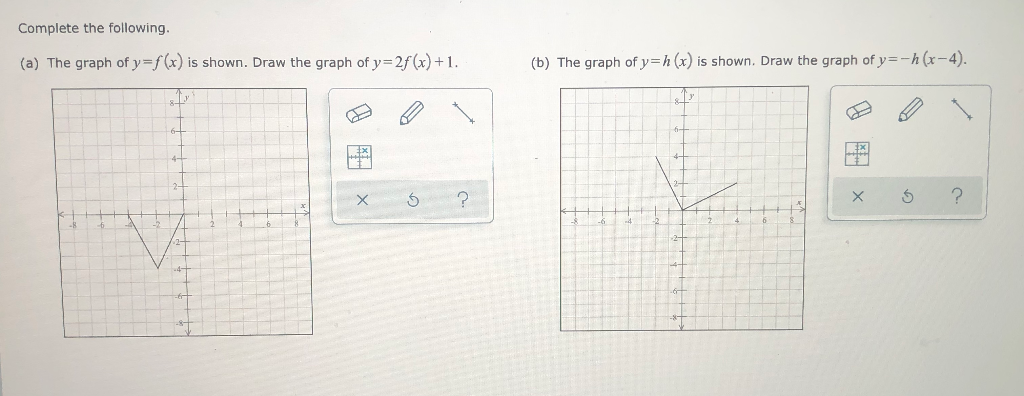 |  |  |
「Y=f(x) graph y=1/2f(x)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
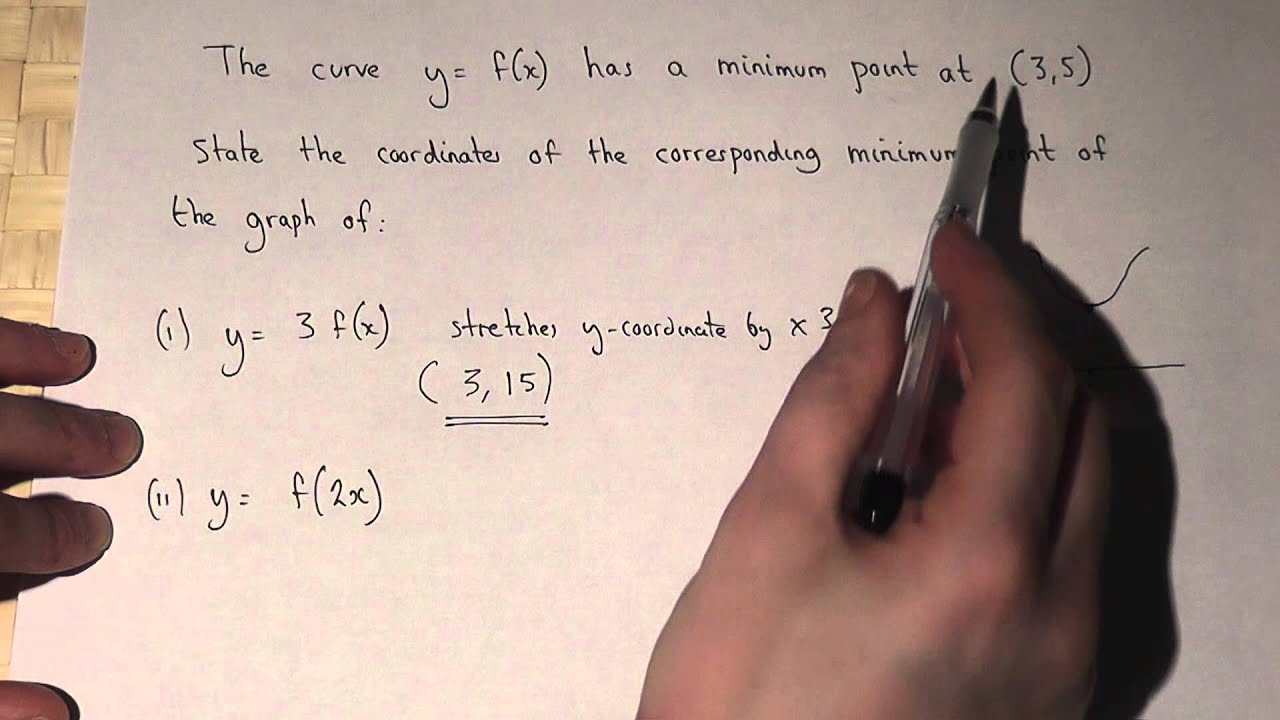 |  | |
 |  |  |
「Y=f(x) graph y=1/2f(x)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「Y=f(x) graph y=1/2f(x)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「Y=f(x) graph y=1/2f(x)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「Y=f(x) graph y=1/2f(x)」の画像ギャラリー、詳細は各画像をクリックしてください。
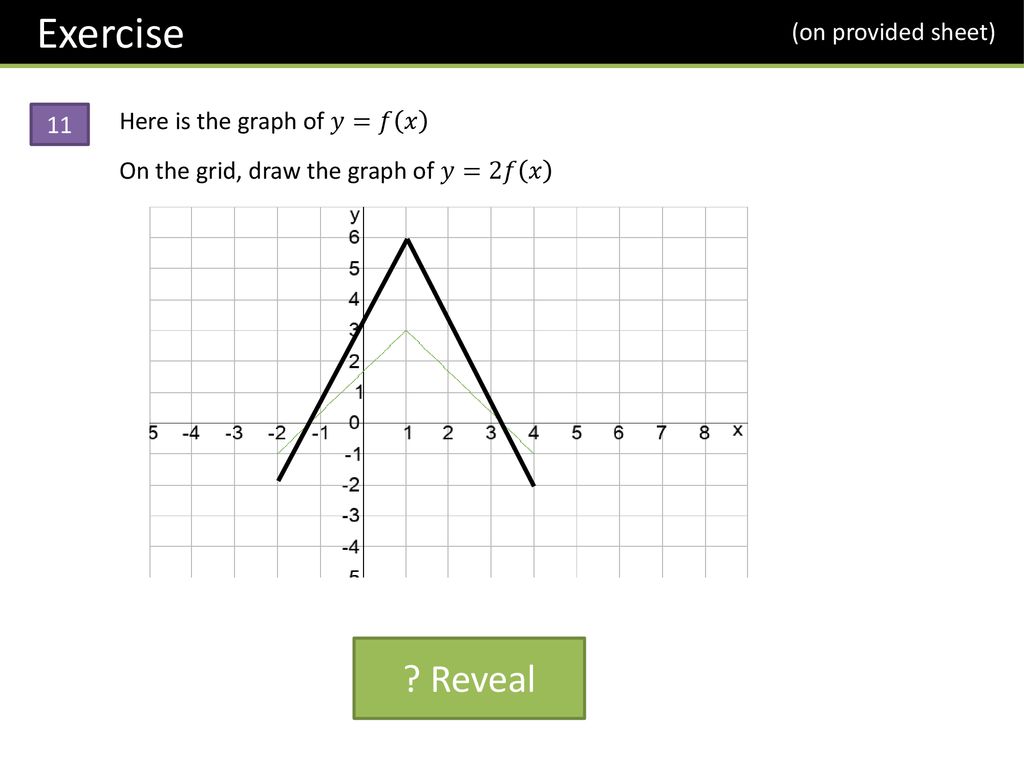 |  | |
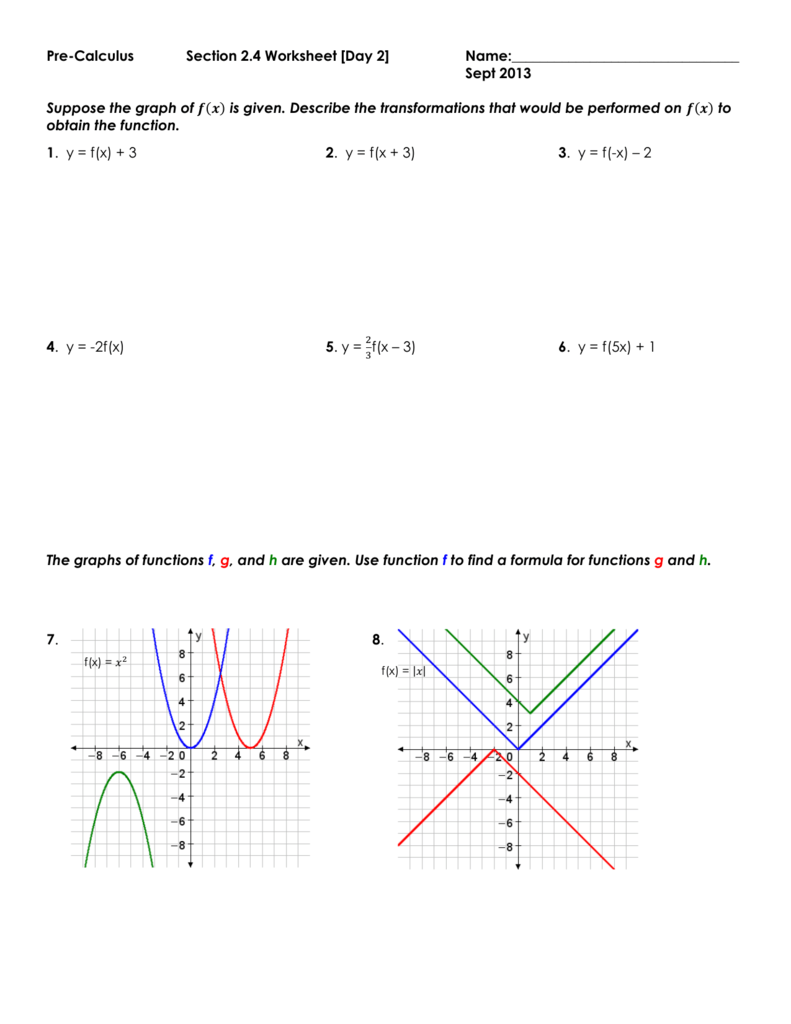 | 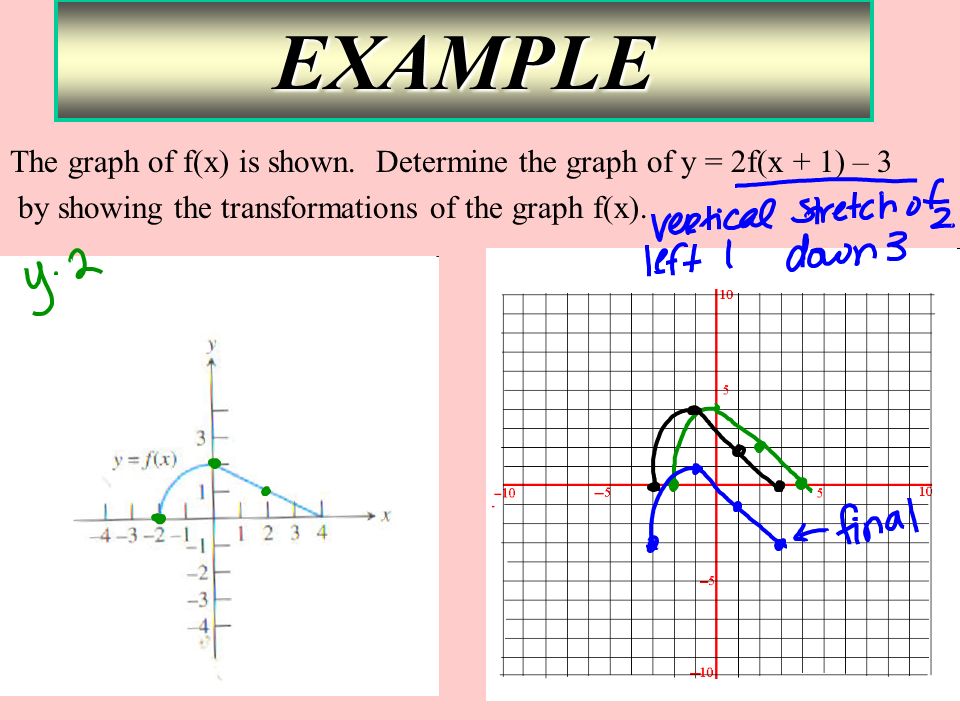 |  |
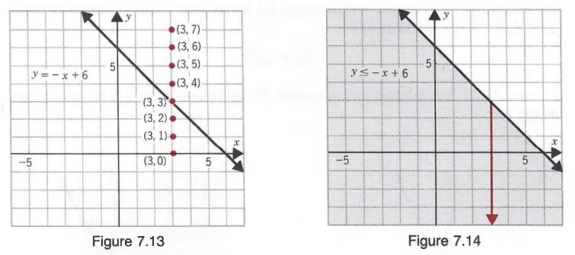 |  | |
「Y=f(x) graph y=1/2f(x)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「Y=f(x) graph y=1/2f(x)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
「Y=f(x) graph y=1/2f(x)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |
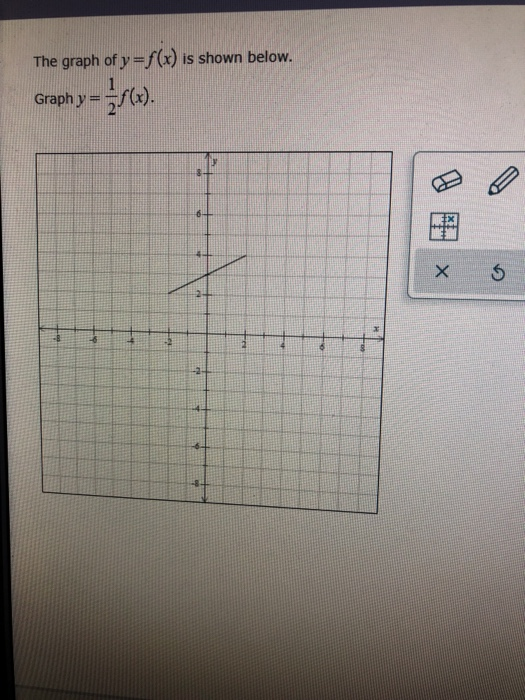
Answer to The graph of y = f(x) is shown below Graph y = 1 over 2 f(x) By signing up, you'll get thousands of stepbystep solutions to your for curves like f(x)=(x3)(x5)(x4) , and then y=1/f(x) , i usually just draw that guide graph of f(x) first, then you should automatically know that all the maxima's will become minima's and vice versa, Always test if its above or below the orignal maxima/minima by
Incoming Term: y=f(x) graph y=1/2f(x), the graph of y=f(x) is shown graph y=1/2 f(x), what does y=2f(x) mean, what does 1/2f(x) do to a graph, how to graph 2f(x), what happens to a graph when y=f(2x),




0 件のコメント:
コメントを投稿